ニュートン法で平方根を求める

ニュートン法は正確には
Newton・Raphson法（ニュ－トン・ラフソン法）といい、
関数 f(x) とその導関数 f'(x) が与えられたとき、方程式f(x)=0 の解を求めるといったもの。
xn+1 = xn - f(x)/f'(x) が収束するまで演算を続ける。

で、今回は平方根をもとめる。

浮動小数版ニュートン法

root(double x){
   double s=1, s2=1;

   do {
        s2=s;
        s=(x/s+s)/2;
   }while(s2!=s);
   return s;
}

整数版ニュートン法

root_i(int x){
    int s=1, s2=1;
    do {
        s=(x/s+s)/2;
        s2=s+1;
        if (s*s<=x && x<s2*s2) break;
    } while(1);
    return s;
}

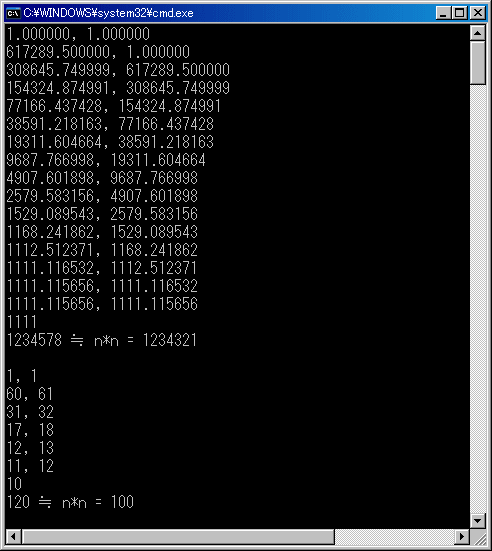
浮動小数版ニュートン法と整数版ニュートン法との違いは評価式。

浮動小数版：s2!=s
整数版： if (s*s<=x && x<s2*s2) break;

整数版の評価式を s2!=s にすると、 120 の平方根を求めようとしたときなど10⇔11で永久ループする。

ニュートン法のサンプル

#include <stdio>

root(double x){
   double s=1, s2=1;

   do {
        printf("%f, %f\n", s, s2);
        s2=s;
        s=(x/s+s)/2;
   }while(s2!=s);
   return s;
}
root_i(int x){
   int s=1, s2=1;
   int cnt=0;

   do {
        printf("%d, %d\n", s, s2);
        s=(x/s+s)/2;
        s2=s+1;
        if (s*s<=x && x<s2*s2) break;
   }while(cnt++<50);
   return s;
}

main(){
   int m, n;
   char s[20];

   m=1234578;
   n=root(m);
   printf("%d\n", n);
   printf("%d = n*n:%d\n\n", m, n*n);

   m=120;
   n=root_i(m);
   printf("%d\n", n);
   printf("%d = n*n:%d\n\n", m, n*n);
}

戻る